Un poliedro es, en el sentido dado por la geometría clásica al término, un cuerpo geométrico cuyas caras son planas y encierran un volumen finito. La palabra poliedro viene del griego clásico, de la palabra πολύεδρον, de poli muchas y edro caras.
Los poliedros se conciben como cuerpos tridimensionales, pero hay semejantes topo lógicos del concepto en cualquier dimensión. Así, el punto o vértice es el semejante topo lógico del poliedro en cero dimensiones, una arista o segmento lo es en 1 dimensión, el polígono para 2 dimensiones; y el polícoro el de cuatro dimensiones. Todas estas formas son conocidas como politopos, por lo que podemos definir un poliedro como un polítopo tridimensional.
Elementos de un poliedro
- Caras: Polígonos que limitan al poliedro.
- Aristas: Segmentos intersección de las caras.
- Vértices: Puntos de intersección de las aristas.
Poliedros regulares
Poliedro regular es aquel que cumple:
- Sus caras son Polígonos regulares iguales.
- Todos los vértices tienen el mismo orden.
- Se llama orden de un vértice de un poliedro, al número de caras (o aristas) que concurren en él.
- Sólo existen un total de nueve poliedros regulares diferentes, divididos en dos familias.
Los poliedros regulares Convexos, conocidos como Sólidos platónicos.
Los poliedros regulares Cóncavos, conocidos como Sólidos de Kepler-Poinsot
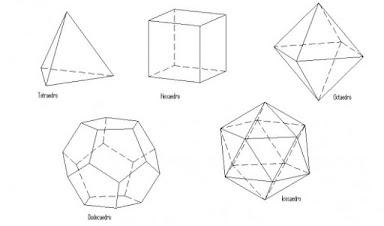
Los sólidos platónicos o sólidos de Platón son poliedros regulares y convexos. Sólo existen cinco de ellos: el tetraedro, el cubo, el octaedro, el dodecaedro y el icosaedro. El nombre del grupo proviene del hecho de que los griegos adjudicaban a estos cuerpos cada uno de los "elementos fundamentales": tierra, agua, aire y fuego, y el restante, el dodecaedro, a la divinidad. Los sólidos platónicos son el inicio del estudio de los poliedros; de estos se derivan los sólidos de Arquímedes y los de Kepler-Poinsot, que a su vez siguen generando más familias.
Los cinco poliedros regulares convexos fueron observados por Platón, quien maravillado por sus propiedades, asoció cada uno de ellos a un "elemento" primigenio de su filosofía (aire, agua, tierra y fuego). Curiosamente, asoció el dodecaedro al "quinto elemento" o ente espiritual de su teoría de la materia. En esta estructura de pensamiento muchos ven la génesis de la teoría molecular, pues muchos elementos cristalinos tienen una estructura atómica que obedece a la forma de tales poliedros
- Figuras de los poliedros regulares convexos
















Gracias!
ResponderBorrarfreggiaro indira
ResponderBorrarJulieta Cano
ResponderBorrarJoana López
ResponderBorrarMichelle Jarenczuk
ResponderBorrarVillalba Milagros
ResponderBorrarGracias profe!
ResponderBorrar